42. 接雨水

Similar Question

Solution Tips

方案一: 按照列求

Loading Question... - 力扣（LeetCode）

var trap = function(height) {
    // 按列求
    let sum = 0;
    //最两端的列不用考虑，因为一定不会有水。所以下标从 1 到 length - 2
    for (let i = 1; i < height.length - 1; i++) {
        let maxLeft = 0;
        // 找出左边最高的
        for (let l = i - 1; l >= 0; l--) {
            if (height[l] > maxLeft) {
                maxLeft = height[l];
            }
        }

        // 找出右边最高的
        let maxRight = 0;
        for (let r = i + 1; r < height.length; r++) {
            if (height[r] > maxRight) {
                maxRight = height[r];
            }
        }

        // 找出两端较小的
        const min = Math.min(maxLeft, maxRight);
        // 只有短板小于当前列的高度才会有水, 其他情况不会有水
        if (min > height[i]) {
            sum += (min - height[i])
        }
    }
    return sum;
};

方案二: 动态规划

官方题解并不好理解, 还是这个好

我们注意到，方案一中。对于每一列，我们求它左边最高的墙和右边最高的墙，都是重新遍历一遍所有高度，这里我们可以优化一下。

首先用两个数组，max_left [i] 代表第 i 列左边最高的墙的高度，max_right[i] 代表第 i 列右边最高的墙的高度。（一定要注意下，第 i 列左（右）边最高的墙，是不包括自身的，和 leetcode 上边的讲的有些不同）

对于 max_left 我们其实可以这样求。

max_left [i] = Max(max_left[i-1],height[i-1])。它前边的墙的左边的最高高度和它前边的墙的高度选一个较大的，就是当前列左边最高的墙了。

对于 max_right 我们可以这样求。

max_right[i] = Max(max_right[i+1],height[i+1]) 。它后边的墙的右边的最高高度和它后边的墙的高度选一个较大的，就是当前列右边最高的墙了。

这样，我们再利用解法二的算法，就不用在 for 循环里每次重新遍历一次求 max_left 和 max_right 了。

var trap = function(height) {
    // 按列求
    let sum = 0;
    //最两端的列不用考虑，因为一定不会有水。所以下标从 1 到 length - 2
    let maxLeft = 0;
    let maxRight = 0;
    for (let i = 1; i < height.length - 1; i++) {
        // 找出左边最高的
        maxLeft = Math.max(maxLeft, height[i - 1]);
        // let maxLeft = 0;
        // for (let l = i - 1; l >= 0; l--) {
        //     if (height[l] > maxLeft) {
        //         maxLeft = height[l];
        //     }
        // }
        // 重复的寻找左右最高的复杂度过高, 想象一下 i++ 之后
        // 其实 maxLeft 只可能是 Math.max(maxLeft, height[i - 1])
        // 能想到这一层的话, 其实就相当于是动态规划压缩了空间了
        // 反过来再去定义 dp[i] 的话, 就是左边最高的值, 和右边最高的值, 分别 dp
        // dp[i] = Math.max(dp[i - 1], height[i - 1])

        // 找出右边最高的, 则是少了一个, 好像得重新找
        // maxRight = Math.max(maxRight, height[i + 1]);
        let maxRight = 0;
        for (let r = i + 1; r < height.length; r++) {
            if (height[r] > maxRight) {
                maxRight = height[r];
            }
        }

        // 找出两端较小的
        const min = Math.min(maxLeft, maxRight);
        // 只有短板小于当前列的高度才会有水, 其他情况不会有水
        if (min > height[i]) {
            sum += (min - height[i])
        }
    }
    return sum;
};

public int trap(int[] height) {
    int sum = 0;
    int[] max_left = new int[height.length];
    int[] max_right = new int[height.length];
    
    for (int i = 1; i < height.length - 1; i++) {
        max_left[i] = Math.max(max_left[i - 1], height[i - 1]);
    }
    for (int i = height.length - 2; i >= 0; i--) {
        max_right[i] = Math.max(max_right[i + 1], height[i + 1]);
    }
    for (int i = 1; i < height.length - 1; i++) {
        int min = Math.min(max_left[i], max_right[i]);
        if (min > height[i]) {
            sum = sum + (min - height[i]);
        }
    }
    return sum;
}

方案三: 双指针

https://www.bilibili.com/video/BV1Qg411q7ia/?vd_source=db8a4b4129af2e1d7a3e3f6357bb4d45

非常 case by case 的一个双指针

方案四: 单调栈

使用单调栈内元素的顺序

从大到小还是从小到大呢？

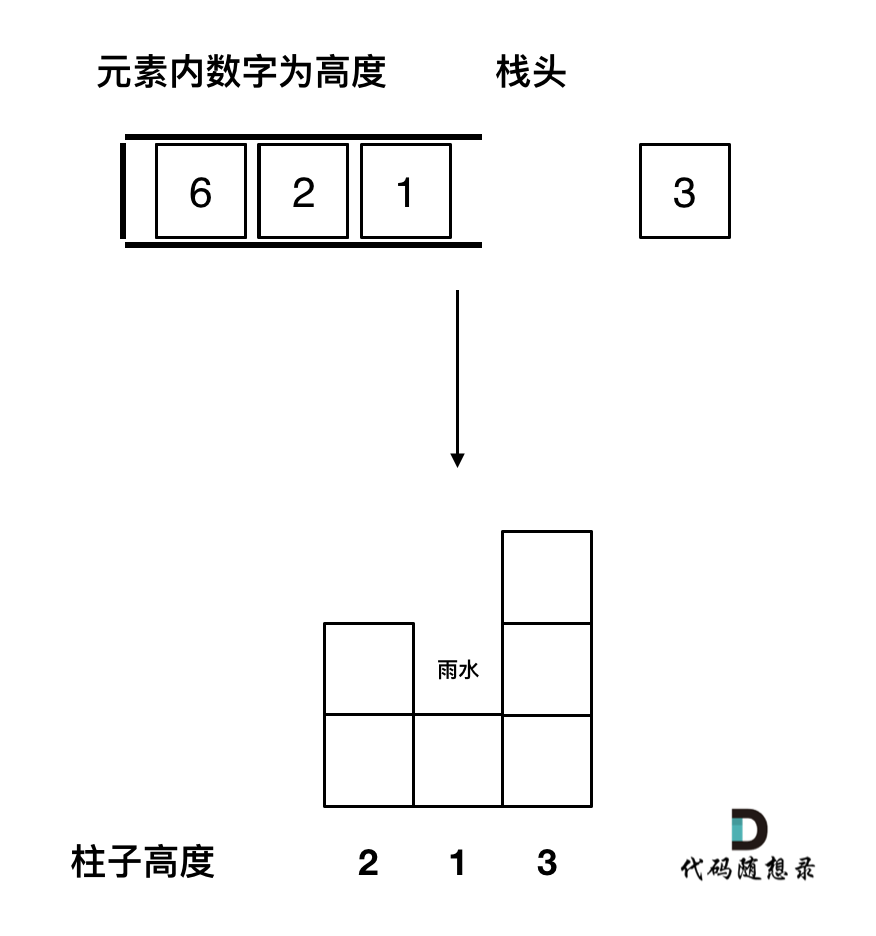
从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。

因为一旦发现添加的柱子高度大于栈头元素了，此时就出现凹槽了，栈头元素就是凹槽底部的柱子，栈头第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。

关于单调栈的顺序给大家一个总结： 739. 每日温度 (opens new window) 中求一个元素右边第一个更大元素，单调栈就是递增的，84.柱状图中最大的矩形 (opens new window) 求一个元素右边第一个更小元素，单调栈就是递减的。

遇到相同高度的柱子怎么办

遇到相同的元素，更新栈内下标，就是将栈里元素（旧下标）弹出，将新元素（新下标）加入栈中。

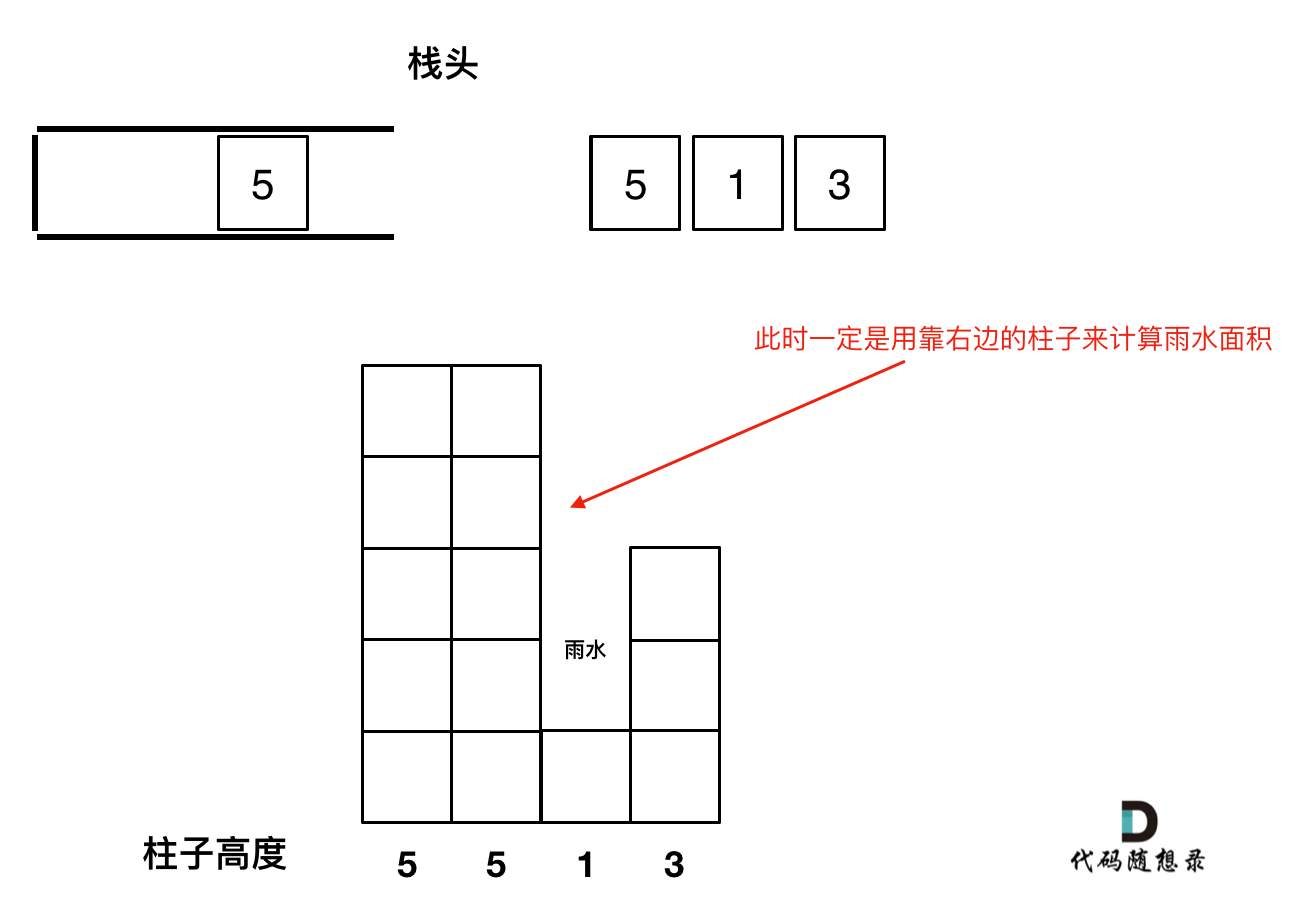
例如 5 5 1 3 这种情况。如果添加第二个 5 的时候就应该将第一个 5 的下标弹出，把第二个 5 添加到栈中。

因为我们要求宽度的时候 如果遇到相同高度的柱子，需要使用最右边的柱子来计算宽度。

栈里要保存什么数值

使用单调栈，也是通过 长 * 宽 来计算雨水面积的。

长就是通过柱子的高度来计算，宽是通过柱子之间的下标来计算，

那么栈里有没有必要存一个 pair<int, int>类型的元素，保存柱子的高度和下标呢。

其实不用，栈里就存放下标就行，想要知道对应的高度，通过 height[stack.top()] 就知道弹出的下标对应的高度了。

所以栈的定义如下：

stack<int> st; // 存着下标，计算的时候用下标对应的柱子高度

明确了如上几点，我们再来看处理逻辑

单调栈处理逻辑

//单调栈 js数组作为栈
var trap = function(height) {
    const len = height.length;
    if(len <= 2) return 0; // 可以不加
    const st = [];// 存着下标，计算的时候用下标对应的柱子高度
    st.push(0);
    let sum = 0;
    for(let i = 1; i < len; i++){
        if(height[i] < height[st[st.length - 1]]){ // 情况一
            st.push(i);
        }
        if (height[i] == height[st[st.length - 1]]) {  // 情况二
            st.pop(); // 其实这一句可以不加，效果是一样的，但处理相同的情况的思路却变了。
            st.push(i);
        } else { // 情况三
            while (st.length !== 0 && height[i] > height[st[st.length - 1]]) { // 注意这里是while
                let mid = st[st.length - 1];
                st.pop();
                if (st.length !== 0) {
                    let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
                    let w = i - st[st.length - 1] - 1; // 注意减一，只求中间宽度
                    sum += h * w;
                }
            }
            st.push(i);
        }
    }
    return sum;
};

//单调栈 简洁版本 只处理情况三
var trap = function(height) {
    const len = height.length;
    if(len <= 2) return 0; // 可以不加
    const st = [];// 存着下标，计算的时候用下标对应的柱子高度
    st.push(0);
    let sum = 0;
    for(let i = 1; i < len; i++){ // 只处理的情况三，其实是把情况一和情况二融合了
        while (st.length !== 0 && height[i] > height[st[st.length - 1]]) { // 注意这里是while
            let mid = st[st.length - 1];
            st.pop();
            if (st.length !== 0) {
                let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
                let w = i - st[st.length - 1] - 1; // 注意减一，只求中间宽度
                sum += h * w;
            }
        }
        st.push(i);
    }
    return sum;
};